My research is in the area of applied and computational mathematics with strong applications in biomedical and industrial problems. I am especially interested in problems where a moving interface is a central issue and where the development of mathematical models and accurate numerical algorithms is needed.
Current Research Topics
Numerical modelling of the cardiac electromechanical activity.
Knowledge of the electrical activity of the myocardium is essential to treat heart diseases and to understand rhythm disorders of the heart. Mathematical modeling could play a crucial role and provide the necessary tools to cardiac researchers.
Results
 Numerical modelling of the electrical wave of the heart with presence of pacemaker.
|
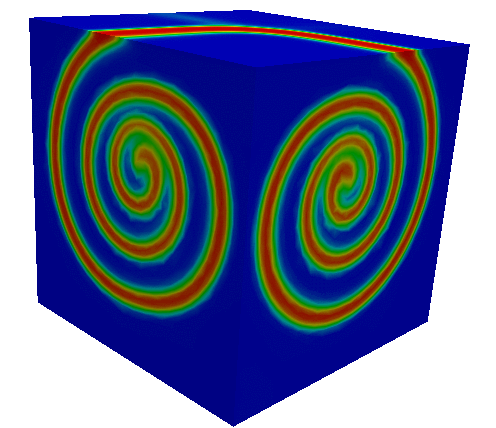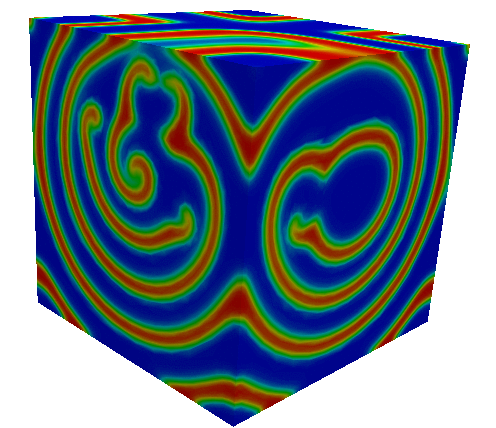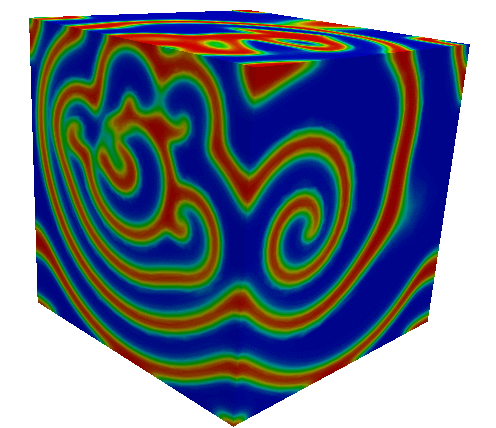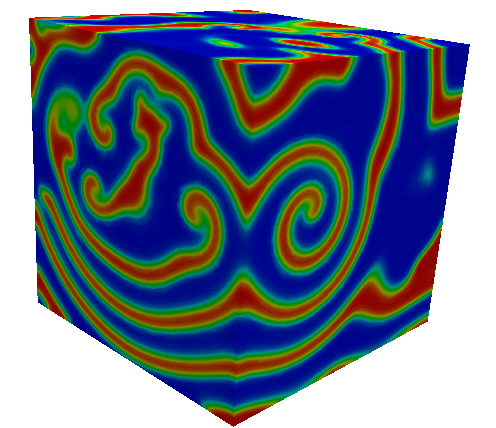 Depolarization-repolarization front for scroll wave turbulent.
|
Mathematical modelling and numerical simulation of phase change problems.
Solid-liquid phase change problems are extremely important in many applications. It is generally recognized that the solid-liquid phase change problems are largely influenced by the natural convection. A classical two-phase Stefan formulation can be used to model this problem coupled with incompressible Navier-Stokes equations.
Results
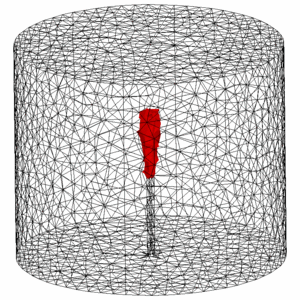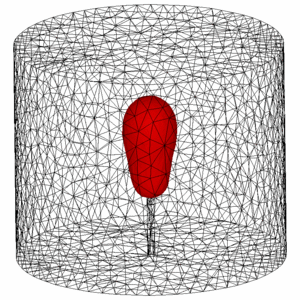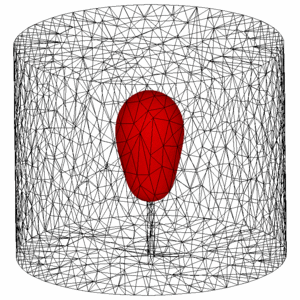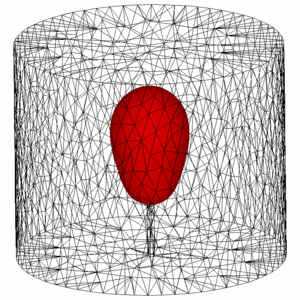 Phase change problem without convection as presented in cryosurgery technique.
|
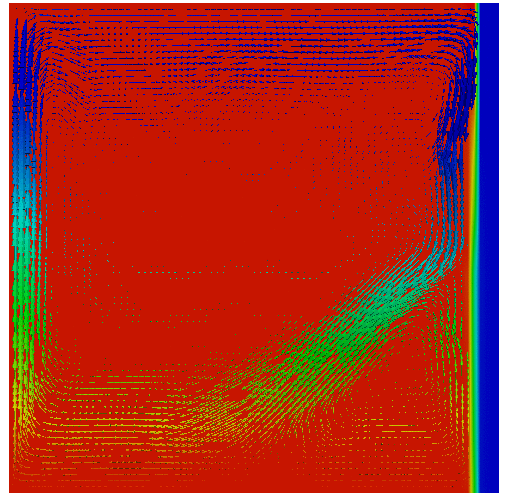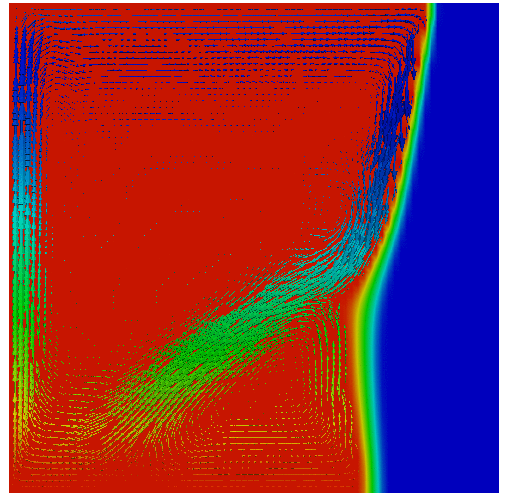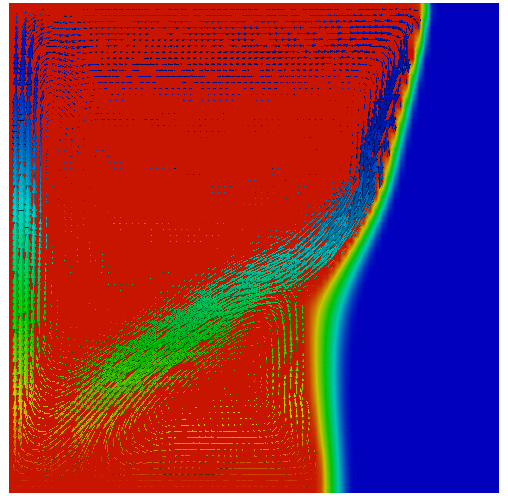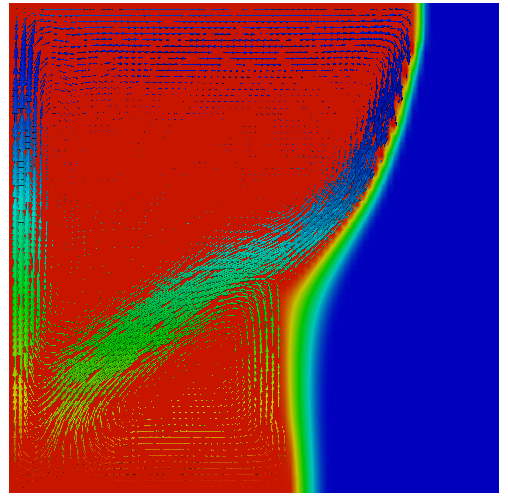 Phase change problem with convection as presented in Water solidification.
|